芜湖长江大桥裕溪河桥为2×80m连续钢桁梁,主桁结构为再分式桁梁,桁高11m,桁宽10m,上弦节间长度为8m,下弦节间长度为4m。该桥通车后,对其运营状态进行检测时,测得桥梁跨中横向振幅较大
[1,2],超过了现行《铁路桥梁检定规范》
[3]限值。
笔者运用文献
[4]建立的列车—桥梁系统耦合振动分析理论和编制的计算软件,采用空间杆系有限元模型分析芜湖长江大桥裕溪河2×80m连续钢桁梁桥的空间自振特性,并对该桥在空载及空重混编货物列车作用下的车桥耦合振动响应进行计算,从保证列车过桥时的安全性和平稳性(舒适性)角度出发,对该桥的横向刚度进行评价。
1 车桥耦合振动分析模型
列车—桥梁空间耦合振动分析模型由车辆计算模型、桥梁计算模型以及车桥之间的轮轨接触关系模型组成。
将车辆与桥梁看作一个联合动力体系,以轮轨接触处为界面,分别建立桥梁与车辆的运动方程,两者之间通过轮轨的几何相容条件和相互作用力平衡条件联系。在具体运用直接积分法来求解车桥系统的动力响应时,分别求解车辆、桥梁的运动方程,用迭代过程来满足轮轨几何相容条件和相互作用力平衡条件。
1.1 机车车辆计算模型
采用二系悬挂多刚体多自由度的机车车辆计算模型,每节车辆由车体、前后转向架以及4个轮对组成,车体与前后转向架各考虑其横摆、浮沉、侧滚、点头和摇头5个自由度,每个轮对仅考虑其横摆和摇头2个自由度,因此,对二系悬挂的4轴机车与客车,每辆车总共23个自由度。
对一系中央悬挂的货车,由于货车采用的是导框式轴箱定位,轴箱和侧架间没有任何弹簧装置,导框与轴箱之间基本没有相对位移,因此,研究货车动力性能时,往往重新建立相应计算模型
[5]。也有为了简单方便
[6],仍采用23个自由度的客车模型,但将轴箱弹簧刚度取大值,并考虑摩擦阻尼的影响(因为货车的中央弹簧除了黏性阻尼外,主要是摩擦阻尼起减振作用)。按车辆动力学,货车中的转8A转向架的摩擦阻尼力按下式计算
[7]:
式中:

表示运动方向,当
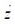
>0时,

=1,当
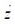
<0时,

=-1;φ为相对摩擦系数,φ=0.067~0.090;K为中央弹簧垂向刚度,K=10.76kN•mm-1;f
st为中央弹簧垂向静挠度,f
st= 35.8mm。
1.2 桥梁计算模型
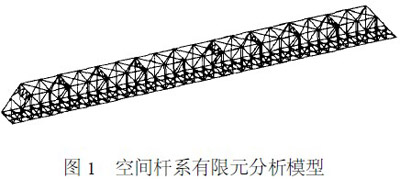
采用空间杆系有限元法对结构进行离散,钢桁架的上下弦杆、腹杆、上下平联、纵横梁、桥门架都按照实际情况全部离散成空间杆单元,离散后的钢桁架共计312 个节点、792 个空间杆单元。桥墩通过计算其墩顶等效纵向与横向水平刚度来加以考虑。建立的计算模型如图1 所示。
桥面二期恒载取2.2 t•m
-1(全桥),将其作为均布质量分配到下弦杆中计算。
1.3 轮轨作用力
根据前述建立车辆动力学模型的有关假定,轮对在竖直方向的运动受钢轨的约束。竖直方向的力为轮对轴重加上轮对惯性力及通过与轮对连接的竖向弹簧和阻尼器传递的弹簧力和阻尼力,轮轨竖向力按杠杆原理分配到相应位置的下弦节点上。在横向,由于轮对在钢轨上存在着蠕滑,轮轨作用力与蠕滑力有关,轮轨横向力采用Kalker非线性蠕滑理论。
由轮轨接触几何学理论及Kalker滚动接触蠕滑理论, 可以给出蠕滑率与蠕滑力/ 力矩的关系
[8],然后由D′Alembert 原理建立轮对的运动方程。由于轮轨法向力是轮对位移的函数,因此,运用迭代法来求解轮轨力(蠕滑力/ 力矩)
[4]。

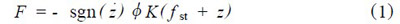
 表示运动方向,当
表示运动方向,当 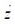 >0时,
>0时,  =1,当
=1,当 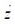 <0时,
<0时,  =-1;φ为相对摩擦系数,φ=0.067~0.090;K为中央弹簧垂向刚度,K=10.76kN•mm-1;fst为中央弹簧垂向静挠度,fst= 35.8mm。
=-1;φ为相对摩擦系数,φ=0.067~0.090;K为中央弹簧垂向刚度,K=10.76kN•mm-1;fst为中央弹簧垂向静挠度,fst= 35.8mm。