近年来，人行桥不断向大跨、轻柔和纤细化方向发展，由此带来世界上许多新建人行桥在人群密集时发生晃动的问题，引起人们对大跨度人行桥人致振动的广泛关注。英国伦敦的千禧桥就是一个最典型的例子。人行桥振动问题本质上是一个多阶动力谐响应问题,但国内的人行桥设计,基本上是借用铁路桥或公路桥规范的动力冲击系数的概念,将其处理为静力等效问题来考虑,这显然是不妥的。本文研究通过在人、车行桥间设置连杆的措施来提高自振频率，确定调频质量阻尼器（TMD）的控制优化参数及验证控制效果，分析大跨人行桥在人行荷载作用下的竖向振动、侧向振动加速度，确定人行桥是否满足舒适度及人致动力稳定要求。

    1.工程概况

    绵阳会客厅一号桥工程位于绵阳会客厅内 “四横”主干道之一—红塔街上，该桥为全长400m的三跨双层斜拉桥，上层为S形人行天桥，下层为双向六车道车行桥，跨径布置为100+200+100m。倒Y型桥塔塔高98m，主体结构高84.5米；车行桥主梁采用大悬臂预应力混凝土箱梁，现场悬浇施工。人行桥主梁采用钢箱梁，采用分段吊装施工，梁宽6.0m，梁高2.0m。斜拉索为单索面，全桥共有68根拉索（其中车行桥52根，人行桥16根）。设计荷载等级为公路Ⅰ级。 

 

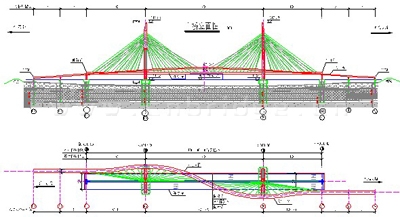
图1  绵阳一号桥布置图（单位：m）

    2.人桥共振分析及舒适性评价

    本工程中的S型人行曲线斜拉桥，自身振动频率较低，在人群步行力的激励下可能会发生共振和行走舒适性不满足要求的情况。这就需要对该桥进行人致振动评估，及研究必要的减振措施（如加装调频质量阻尼器）来减小桥梁的振动。

    2.1 建立模型

    根据原设计方案，人行桥与车行桥两桥共享桥塔，其它部位都无连接。采用Midas建立绵阳一号桥全桥有限元模型。车行桥主梁、人行桥主梁、桥塔采用梁单位模拟，拉索采用杆单元模拟，二期恒载通过质量单元模拟，车行桥主梁节点与其拉索采用刚臂连接。对于边界条件，将桥塔基础模拟为固结；车行桥和人行桥梁端边支座处的竖向、横向和扭转自由度约束，其它自由度释放；车行桥为纵漂体系，在塔梁连接处，车行桥节点和塔节点具有相同的竖向、横向和扭转位移；在人行桥的梁与一个塔的牛腿通过固定支座连接。

    在动力特性有限元分析中，首先考虑主缆的初始应变与结构自重并考虑几何非线性进行静力分析，然后在静力分析的基础上得到结构的初应力刚度矩阵后再进行特征值与特征向量求解，得出结构的自振频率与按各阶模态位移最大值规一化的振型。

    分析计算结果可以得到：人行桥横向振动的一阶频率为0.4588Hz，振型特点是主跨正对称侧弯，二阶频率为0.7314Hz，振型特点为主跨反对称侧弯同对称竖弯；人行桥竖向振动的一阶频率为0.4684Hz，振型特点是主跨对称竖弯，二阶频率为0.7117Hz，振型特点为主跨反对称竖弯，竖向振动频率密集；对只有人行桥参与振动的振型，广义质量小，阻尼也低，发生共振时容易发生大幅振动。

    本桥的一阶侧向模态频率跟伦敦千禧桥很接近，因此同样容易发生大幅侧向振动。但主梁（包括桥面等）恒载达到48.4kN/m，是千禧桥的一倍以上。因此可以推测发生大幅振动的行人数比千禧桥要高。本桥的特点是曲线梁桥，竖向振型总是伴随着横向振动，有时耦合非常严重。因此抑制横向振动和竖向振动同等重要，而且需要抑制振动的频率范围很宽，敏感模态个数多。

    2.2 舒适度评价

    考虑到很多人行桥的竖向振动频率位于振动敏感区间，通过频率调整来满足人行桥的振动舒适性要求很难做到，因此我们通过限制动力响应值（主要是加速度）来满足行走舒适性要求。通常采用单自由度（模态）模型或者有限元三维模型，以单人和人群共振荷载情况下结构所产生的最大加速度响应来评估其振动舒适性。若最大加速度响应小于行人能够承受的最大加速度，则认为人行桥的人致振动问题满足要求。否则，应该对结构进行修改或者安装阻尼减振设备。本文采用的行走舒适性指标见表1。
 

表1 人行桥的加速度舒适性指标
 

    
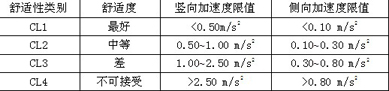
    通过计算结果知道：绵阳一号桥人行桥振动频率中，第2阶及第5阶频率均为有明显横向振动分量的模态，且位于横向敏感频率范围，需要计算结构侧向荷载共振时的最大加速度响应。第14、15、17、18、19和20阶模态为人行桥的竖向振动模态，频率分别为1.620Hz、1.678Hz、1.832Hz、1.960Hz、2.392Hz和2.410Hz，正好在人行步频范围内，发生竖向共振可能性也是非常大的，第14阶和第15阶模态为竖弯、侧弯严重耦合模态，发生竖向共振时还可产生很大的侧向加速度。

    按单自由度方法对各敏感模态计算模态共振时的加速度响应可以得到2阶侧弯和6阶竖弯敏感模态分别发生共振时的最大竖向和侧向加速度响应、及满足最好舒适度指标的时候需要的各阶模态阻尼比。
 

表2 自由行走状态主要模态共振时的最大加速度响应（m/s2）
 

   
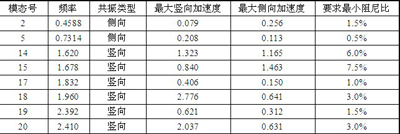
    3.减振方案设计

    通过上述分析知道，绵阳一号桥人行桥振动频率中，第2阶及第5阶频率位于横向敏感频率范围，需要计算结构共振下的最大加速度响应。第14、15、17、18、19和20阶模态为人行桥的竖向振动模态正好在人行步频范围内，共振可能性也是非常大的。对于原结构设计方案的人致振动分析结果，针对各阶模态设计了两种减振方案。

    3.1 TMD减振设置方案

    以控制第2阶模态的TMD减振装置为例，说明TMD参数设计方法。

    根据模态分析结果，第2阶横向振动模态的频率f=0.4588Hz，相应的模态质量m*＝573.8吨，TMD安装于横向模态位移最大处即在主跨跨中，TMD的运动方向为横桥向。TMD的质量与第一阶横向振动模态的广义质量比值μ取为6.0%。
 

   
    达到最优控制效果时，TMD系统的频率和模态阻尼比分别为
 

    因此，TMD系统的刚度和阻尼系数分别为
 

    全桥设置6套TMD系统，针对原设计方案的TMD装置参数及安装位置如下表所示：
 

表3 针对原设计方案的TMD装置参数及安装位置
 

   
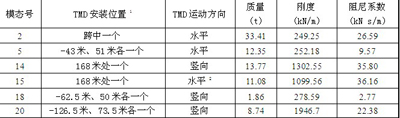
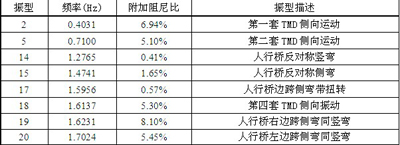
    对设置了上述6套TMD系统的人行桥进行了减振控制仿真，表4给出了由复特征值分析得到的安装减振系统后人行桥的敏感频率与TMD附加的阻尼比。从表4中可以看出，各阶敏感频率的模态阻尼比都有很大提高，基本满足减振要求。
 

表4 原设计方案附加减振装置后的敏感频率与振型描述
 

（未完）

    参考文献：

    [1] 孙利民，闫兴非.人行桥人行激励振动及设计方法.《同济大学学报（自然科学版）》，2004，32（8）：996—999

    [2] 陈政清，华旭刚  《人行桥的振动与动力设计》