近年来,随着我国现代化建设的快速发展,交通运输业蓬勃兴起,高速公路、城市立交桥和高架桥13益增多,促进了大量斜、弯桥梁的出现。斜、弯梁桥不仅能很好地适应地形地物的限制,而且由于其结构线条平顺、流畅、明快,给人以美的享受,同时,为了改善道路的线形及适应城市的街道条件,往往采用斜弯桥跨越更为合理。
在斜、弯梁桥中,横梁对于加强结构的整体性、加强主梁横向联系、改善主梁之间的荷载横向分配性能有不可忽视的、作用。用横粱分析法简化粱桥空间计算就是一种可取的思路 然而在有关文献介绍的方法中,把横梁当作静定结构来计算,这些方法对宽跨比较小的桥梁结构引起的误差不太大,但对宽跨比较大的桥梁则不大适用。
梁格分析法在考虑斜、弯梁桥弯扭耦合作用的基础上,根据各梁的弹簧系数建立的线性方程,导出计算斜、弯梁桥各主梁荷载及内力横向分布影响线的基本公式,在求得的内力影响线上横向加载,就可求得主梁的荷载横向分布系数,从而可按直梁桥计算步骤算出主梁和横梁的各项内力。
1、梁格法基本理论
1.1 基本假定
(1)梁横截面各项尺寸与跨长相比很小,即可将实际结构视为集中在梁轴线上的弹性杆件;
(2)平截面假定,即梁变形后横截面仍保持为平面;
(3)刚性截面假定,即梁变形后横截面无畸变;
(4)梁中截面翘曲扭转所引起的正应力和剪应力,与基本弯曲和纯扭转的应力值相比很小,可忽略不计,只计纯扭转的影响。
1.2 梁格分析法的力学模型
广义梁格法的计算模型是,将横梁看作支承在主梁上的弹性支承连续梁(主梁即为弹性支座),同时,横梁各支座处的弹簧常数均是变化的,基本图式如图1。
1.3 竖向力和扭矩的线性方程组的建立根据各结点的竖向、扭矩的平衡可建立线性方程组,如式(1)
1.4 主梁内力横向分布影响线值的计算
利用式(1)求得各主梁的竖向反力
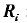
和集中扭矩
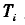
的影响线,代人各主梁纵向弯矩、剪力、扭矩的计算公式(由结构力学方法求得)或纵向影响线中的相应数值(由有限元方法求得),即可求得各主梁在计算截面处的横向弯矩、剪力和扭矩。
求得的内力即为荷载P=1作用下各主梁下各主梁在所受荷载R 和 作用下的横向内力值,然后,利用式(2)即可求得横向内力影响线,这样就可按荷载横向分布的方法来计算了。
式中,
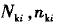
分别为M,Q,T对应的横向内力值和横向内力影响线值。
由于弯扭耦合作用,各主梁分配的荷载,不仅有竖向力, 还有扭矩 。因而,一般的作法是,采用先计算竖向荷载和扭矩荷载的横向分配(简称荷载横向分布系数),再利用混合影响线在纵向加载求得总内力;然后直接计算主梁的内力横向分布(简称内力横向分布系数)。
式中:j为计算梁号;k为车队数;2k为车轮数;

为主梁j在P=1作用于计算截面时的弯矩;
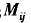
为内力横向系数,见式(3)。
式中:j为计算梁号
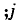
为荷载作用位置;

为主梁j在R=1作用下计算截面的弯矩;
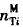
为主梁j在

=1作用下计算截面的弯矩。
2、计算示例
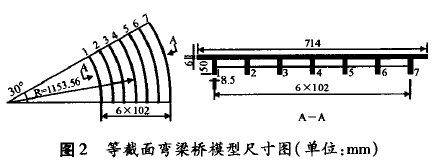
本例采用文献[1]中的有机玻璃模型试验,其基本数据见表1,具体尺寸见图2,并在有限元软件中采用梁格法建立模型计算。
3、结论
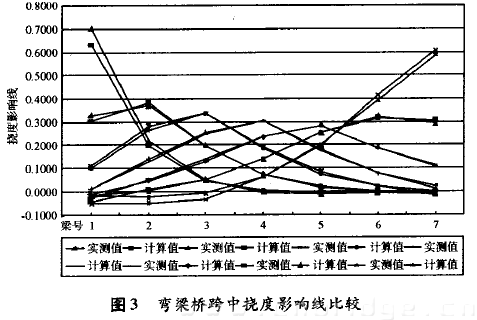
从图3有限元软件梁格法建模分析的结果与有机玻璃模型试验结果对比分析可以看出,梁格法应用于斜、弯梁桥是一种实用简便的计算方法,又是一种比较精确的计算方法。


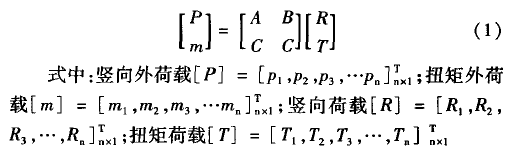

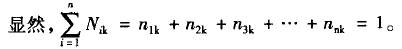
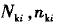 分别为M,Q,T对应的横向内力值和横向内力影响线值。
分别为M,Q,T对应的横向内力值和横向内力影响线值。

 为主梁j在R=1作用下计算截面的弯矩;
为主梁j在R=1作用下计算截面的弯矩;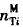 为主梁j在
为主梁j在