引 言
双曲拱桥是我国20世纪60~70年代常用的一种拱桥形式,由于该类拱桥结构整体性差,施工质量变异大,设计荷载标准偏低,随着交通量和车辆载重的增加,桥梁长期处于超载和大交通量条件下运行,至今几乎所有的双曲拱桥都出现不同程度的病害,对该类桥型的加固改造工程屡见不鲜。由于时间上的差异性及加固前后结构特点的差异性,对于双曲拱桥承载能力评估及分析的标准是工程界经常讨论的话题,归纳为以下两点:
(1)由于计算方法的限制,20世纪60~70年代设计双曲拱桥时,内力计算多采用经典力学方法
手算,即应用结构力学及相关桥梁工程知识把主拱圈看成裸拱进行计算分析,该方法很难解决高次超静定问题,而且存在大量的假设,不考虑拱上联合作用,也很少考虑连拱效应等,使得计算结果与实际结构存在一定的差别。
(2)桥梁设计规范在近50年内经过多次修改,大跨度桥梁应按照现行设计规范进行加固设计,因此必然存在荷载等级的区别,加固前后结构强度刚度分析标准同样也存在区别。
1 工程概况
某大桥位于湖北省境内,如图1所示,该桥为主跨90m的钢筋混凝土变截面悬链线无铰双曲拱桥,全长116.3m,矢跨比1/8,设计拱轴系数为2.814,变厚系数0.13,桥宽布置为净8m+2×1.0m, 全宽l0m。主拱圈构造为五肋四波悬半波,原设计荷载为汽-20级、挂-100级,人群荷载2.5kN/?。

图1 加固前大桥近景
1.1 主要病害
该桥1979年竣工通车,至今已有30年。由于原桥设计、施工以及后期超负荷运营等原因,导致目前该桥出现一定程度的病害。经过检查,主要病害情况如图2~4:
(1)主拱圈拱波顶部普遍发现纵向裂缝,最长约2m,沿裂缝有明显的渗水痕迹;腹拱圈微弯板有多处纵向裂缝,漏水现象严重,多数纵向裂缝已贯通整个腹拱,且裂缝较宽,最大达1mm。
(2)桥面破损严重,局部有坑槽,横坡、纵坡不平顺,行车条件较差;人行道缺损严重;全桥栏杆基本都有破损,混凝土剥落情况严重,多处露筋。
该桥主拱肋为整体现浇,调查表明主拱肋总体情况较好,无明显裂缝,但有局部破损。由以上调查结果可知该桥的主要病害体现在主拱圈拱波顶部纵向开裂,拱肋间的横向联系薄弱,桥梁的整体工作性能差,腹拱结构破损严重,但作为拱桥承重结构的主拱肋的受力状况基本处于弹性阶段,若能采取局部补强进行加固处理,则主拱圈仍具有相当的承载能力。

图2 主拱拱波纵向裂缝 图3 腹拱贯通纵向裂缝

图4 桥面系严重破损
1.2 加固措施
根据对桥梁的结构特点及主要病害分析结果,按以下原则提出加固方案:通过维修加固补强,消除桥梁现有病害,提高桥梁承载力和耐久性,使加固后的桥梁满足正常使用要求,荷载等级达到公路-Ⅱ级。主要加固方法(见图5)如下:
(1)主拱圈实腹段局部加固
由于原桥的主拱圈采用双曲拱形式,结构本身横向刚度不大,实腹段跨中区域拱波已出现纵向裂缝。通常多采用增加肋间横梁等方法提高结构整体刚度,但此种方法一定程度上破坏了主拱肋结构,本文提出一种主拱圈实腹段局部加固的方法,先拆除侧墙和拱上填料,凿毛拱板,待表面清洗干净后,植入锚筋,再在其上浇注8cm厚C40钢筋混凝土板。锚筋将钢筋混凝土板与拱板连为整体,从而增大拱板受力面积,使其强度提高,同时也增强了拱圈的横向联系。
(2)更换腹拱圈加固
将原双曲拱式腹拱改成板拱式腹拱,即拆除腹拱,保留拱上横墙并将其加高至设计标高,再在横墙上整体现浇30cm厚钢筋混凝土板拱,这样既达到增强腹拱圈横向联系,改善结构受力状态的目的,同时也替换了原桥严重破损的腹拱。
(3)更换填料,重新铺设桥面系
拆除原桥面系,包括桥面铺装、人行道和栏杆;拆除侧墙、拱上填料和腹拱拱圈。待实腹段加固和腹拱加固完成后,铺设防水层,浇筑侧墙,分层铺设轻质填料,安装护栏,重新进行桥面铺装,改善桥面行车性能。
(4)其他构件维修养护
对主拱圈的拱波、横隔板及腹拱墩的裂缝采用灌注环氧树脂的方法封闭处理;对主拱圈、横墙表面破损的处理方法是先将钢筋锈迹清除,并把松动的保护层凿去,洗净。如损坏面积不大,可用环氧砂浆修补;如损坏面积过大,可喷注高标号水泥砂浆。
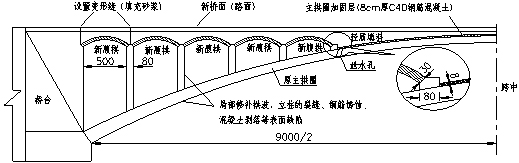
图5 全桥局部加固部位
2 承载能力分析讨论
2.1 计算方法对拱桥承载力分析的影响
早期设计的双曲拱桥以经典力学计算方法为主,且引入一定假设,通常按照弹性支承连续梁算法计算出每根拱肋的横向分配系数,之后再进行内力计算,最后进行承载力分析验算,计算过程中不考虑拱上建筑刚度的贡献,造成了设计结构具有偏安全的特点,这也是该类桥型在后期超载能力较强的主要原因,大量理论研究表明,传统的拱桥计算方法,难以准确反映其实际承载能力。
有限元技术的发展使得结构承载力的计算分析快速、简单、准确,只需按照结构实际线形及尺寸并选择合适的单元建立结构空间有限元模型,不需引入假设计算拱肋的横向分布系数,同时还可将拱上建筑及桥面系结构一并建入有限元模型中,这样便可充分验算全桥的承载能力。对于双曲拱桥,梁格法模型是目前常用的计算模型,在拱肋、拱波及拱板之间结合状态良好的情况下,可以把每个拱肋和相应的拱板看成一个个纵梁,横向刚度通过虚拟横梁模拟,应用梁格法建立双曲拱桥模型,能够达到符合实际结构受力特点的要求[1]。
以上两种计算方法可以用图6对比表示,①表示计算示例桥型;②是采用传统计算方法的简图,实腹段填料采用曲线均布荷载处理,空腹段立柱处施加集中力荷载,只采用裸拱模拟;③是采用有限元方法并考虑拱上建筑的计算图式,只有填料及桥面系结构采用均布荷载模拟,某些情况下,为评定结构的准确受力状态,还可以将侧墙桥面系等构造一并采用有限元程序模拟。
2.2 加固前后设计荷载等级的影响
综合考虑区域经济发展及交通量需求,加固桥梁可能会涉及到提高荷载等级、拓宽等因素,而且现行设计规范下的荷载等级与旧规范所采用的荷载等级有着一定的差别;早期拱式结构承载力分析方法与新规范制定的承载力分析方法也有着差异。
本文加固桥梁原设计荷载等级为汽车-20级,加固设计荷载等级应该满足公路-Ⅱ级。利用有限元方法计算出结构主要控制截面在以上两种荷载等级下的内力结果如图7所示,从对比图可以看出,在两种荷载等级下的结构内力基本保持一致,说明旧规范的汽车-20级与新规范的公路-Ⅱ级比较接近,在主拱结构基本没有病害的情况下,将桥梁加固后荷载等级定为公路-Ⅱ级是可取的。
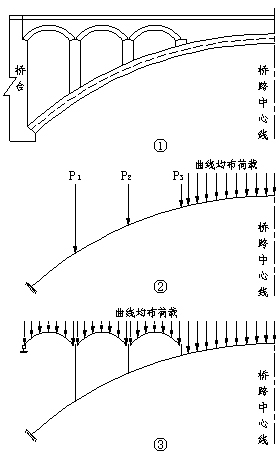
图6 拱桥计算简图
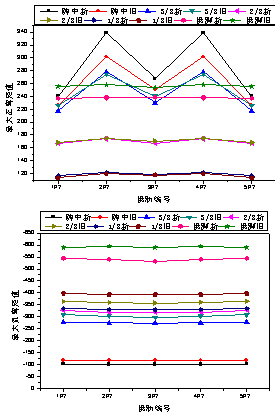
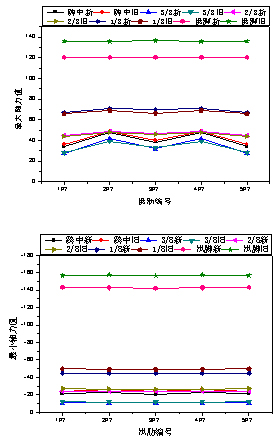
图7 拱桥计算简图
3 承载能力计算分析
3.1 有限元模型建立
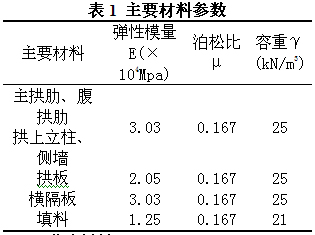
由于本桥为变截面悬链线无铰拱桥,根据《公路桥涵设计通用规范》(JTG D60-2004)的建议,为准确判断该桥的承载能力现状,在计算时考虑拱上建筑与主拱圈的联合作用。采用桥梁专用有限元分析软件Midas/Civil利用加固后结构实测主拱肋线形建立全桥杆系有限元模型(如图8),全桥共分为6126个节点,9615个单元,全结构采用梁、板单元模拟,腹拱采用板单元模拟,其余均采用梁单元模拟。边界条件处理为:在主拱肋拱脚处设固定支座,边腹拱靠桥台侧拱脚处设铰支座,主要材料参数见表1。

图8 Midas/Civil有限元模型
3.2 承载力计算
《桥规》[2]规定,拱圈内力系按分项安全系数的极限状态原则设计,其设计原则是:荷载效应不利组合的设计值
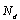
小于或等于结构抗力效应的设计值
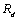
。拱圈为偏心受压构件,其正截面抗压强度按下列公式计算:
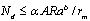
式中,
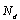
为荷载效应不利组合设计值;
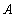
为构件截面面积;
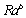
为材料抗压标准强度;
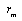
为材料安全系数,按《桥规》采用;
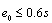
为纵向力的偏心影响系数。
对于单向和双向偏心受压构件,受压偏心距的限值在基本组合情况下应该满足
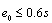
[3]。式中,
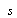
表示截面重心轴至偏心方向截面边缘的距离。按此方法可以判断出所有不利截面的结构抗力与设计内力之间的关系,从而得出全桥的整体承载能力状态。取主拱圈最边肋拱脚、L/2、L/4截面及最不利L3/8截面为控制截面进行验算,验算荷载等级为公路-Ⅱ级。桥梁主拱圈抗力效应如表2所示。
计算结果表明:加固后各验算截面的偏心距均小于规范限值0.6
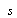
,加固后结构各验算截面的计算值均小于抗力值,且安全储备较大。
4 结论
旧规范的汽车-20级与新规范的公路-Ⅱ级两种荷载等级下的结构内力计算结果基本保持一致,说明在主拱结构基本没有病害的情况下,通过局部增大主拱圈截面,更换腹拱圈,减轻结构自重等加固改造措施,可有效消除桥梁的病害,提高桥梁的承载力,经计算表明,桥梁荷载等级达到公路-Ⅱ级要求。
表2 加固后主拱圈抗力效应
截面
|
荷载效应
|
偏心距
|
|
抗力(kN)
|
容许偏心距 (m)
|
判断
|
组合
|
M(kN.m)
|
N(kN)
|
(m)
|
拱脚
|
恒载+公路-Ⅱ级max
|
72.64
|
4358.75
|
0.02
|
0.98
|
7250.58
|
0.40
|
Yes
|
恒载+公路-Ⅱ级min
|
-320.22
|
5352.38
|
-0.06
|
0.83
|
6122.08
|
-0.40
|
Yes
|
1/4L
|
恒载+公路-Ⅱ级max
|
68.61
|
3182.47
|
0.02
|
0.97
|
5124.69
|
0.29
|
Yes
|
恒载+公路-Ⅱ级min
|
-12.32
|
3770.81
|
-0.01
|
1.00
|
5256.59
|
-0.29
|
Yes
|
1/2L
|
恒载+公路-Ⅱ级max
|
87.72
|
663.97
|
0.13
|
0.50
|
1654.9
|
0.18
|
Yes
|
恒载+公路-Ⅱ级min
|
25.47
|
860.80
|
0.03
|
0.95
|
3141.68
|
0.18
|
Yes
|
3/8L
|
恒载+公路-Ⅱ级max
|
91.95
|
2065.05
|
0.04
|
0.85
|
2940.4
|
0.21
|
Yes
|
恒载+公路-Ⅱ级min
|
23.23
|
2739.03
|
0.01
|
0.94
|
3140.3
|
0.21
|
Yes
|
参 考 文 献:
[1] 黄侨,葛占钊,林阳子.梁格法在双曲拱桥承载能力评估中的应用[J]. 中外公路.2007(6): 89-93.
[2] JTG D60-2004,公路桥涵设计通用规范[S].
[3] 顾懋清,石绍甫.公路桥涵设计手册-拱桥[M].北京:人民交通出版社,1996.










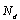 小于或等于结构抗力效应的设计值
小于或等于结构抗力效应的设计值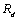 。拱圈为偏心受压构件,其正截面抗压强度按下列公式计算:
。拱圈为偏心受压构件,其正截面抗压强度按下列公式计算: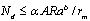
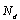 为荷载效应不利组合设计值;
为荷载效应不利组合设计值;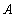 为构件截面面积;
为构件截面面积;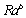 为材料抗压标准强度;
为材料抗压标准强度;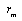 为材料安全系数,按《桥规》采用;
为材料安全系数,按《桥规》采用;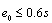 为纵向力的偏心影响系数。
为纵向力的偏心影响系数。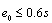 [3]。式中,
[3]。式中,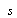 表示截面重心轴至偏心方向截面边缘的距离。按此方法可以判断出所有不利截面的结构抗力与设计内力之间的关系,从而得出全桥的整体承载能力状态。取主拱圈最边肋拱脚、L/2、L/4截面及最不利L3/8截面为控制截面进行验算,验算荷载等级为公路-Ⅱ级。桥梁主拱圈抗力效应如表2所示。
表示截面重心轴至偏心方向截面边缘的距离。按此方法可以判断出所有不利截面的结构抗力与设计内力之间的关系,从而得出全桥的整体承载能力状态。取主拱圈最边肋拱脚、L/2、L/4截面及最不利L3/8截面为控制截面进行验算,验算荷载等级为公路-Ⅱ级。桥梁主拱圈抗力效应如表2所示。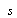 ,加固后结构各验算截面的计算值均小于抗力值,且安全储备较大。
,加固后结构各验算截面的计算值均小于抗力值,且安全储备较大。

